G2Aero Software: Aerodynamic Shape Parametrization Using Separable Shape Tensors

NREL's data-driven G2Aero framework uses a matrix (2-tensor) manifold to parametrize (learn) a manifold of airfoil shapes for wind turbine blade design.

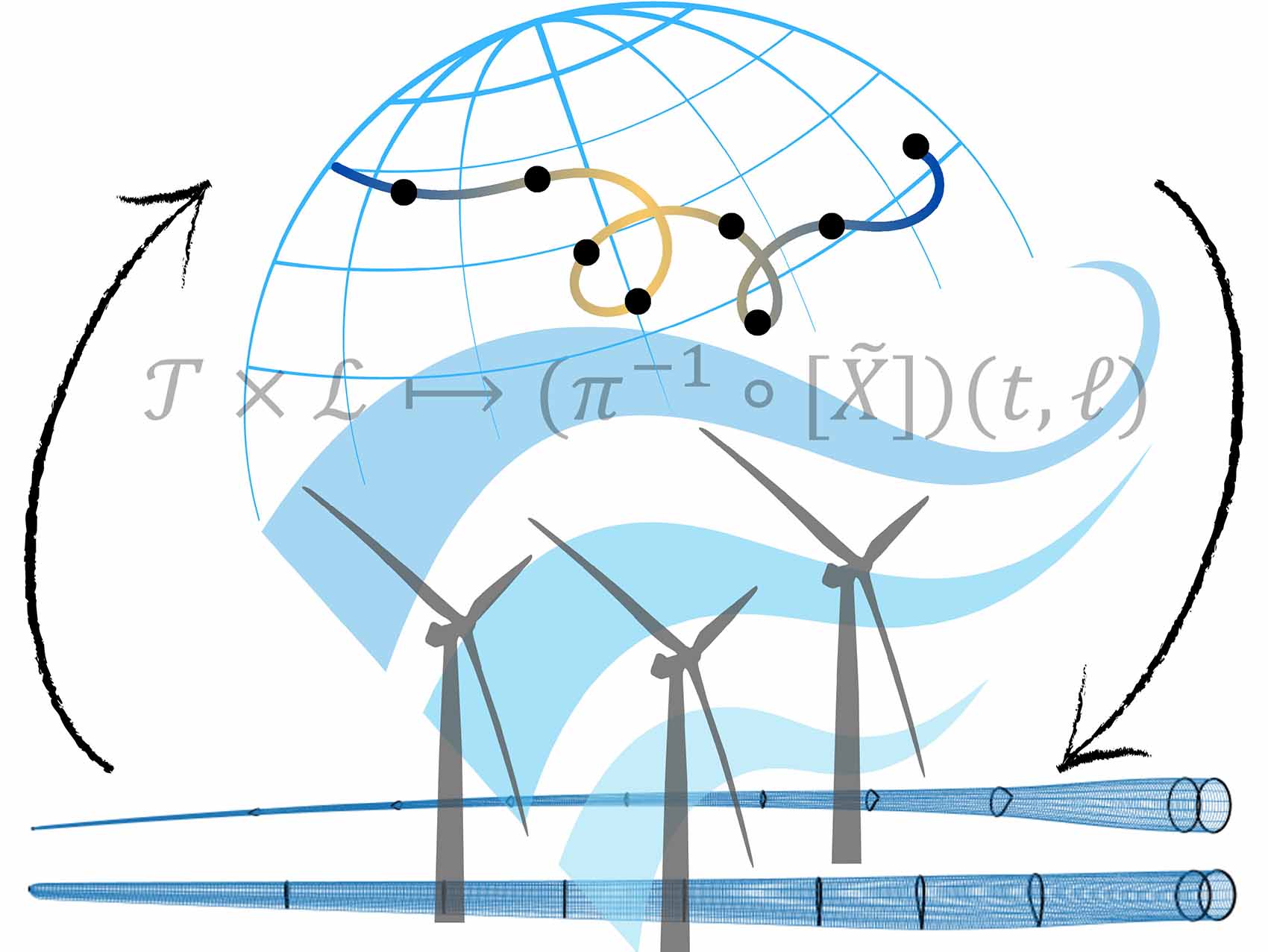
Notable functionalities of the G2Aero software include:

• Generating novel 2D airfoil shapes informed by a database of physically relevant airfoils
• Building 3D blades by interpolating sequences of 2D airfoil cross-sections
• Generating blades with consistent perturbations along the blade span

The separable shape tensors method utilizes a topology of product manifolds to inform parametrization of 2D and 3D aerodynamic shapes using a data-driven approach.

Although airfoil shapes have been studied extensively, their representation and design are complex due to their extreme operating conditions and the highly sensitive relationship between shape deformations and changes in aerodynamic performance.

Many artificial intelligence-aided design and manufacturing algorithms rely on shape representation methods to manipulate shapes. These algorithms can significantly benefit from shape representation that better regularizes deformations and reduce the dimension of the design space.

Novel aerodynamic shape parametrization was developed as a part of ARPA-e INTEGRATE project.

Airfoils generated by G2Aero were coupled with NREL's WISDEM: Wind-Plant Integrated System Design Engineering Model (GitHub) to design blade shapes with reduced costs of energy compared to traditional design methods.

Publications

Invertible Neural Networks for Aerodynamic Design of Wind Turbine Blades, NREL Presentation (2023)

Separable Shape Tensors for Aerodynamic Design, Journal of Computational Design and Engineering (2023)

Grassmannian Shape Representations for Aerodynamic Applications: Preprint, NREL Conference Paper (2022)

Contacts